GEOMETRIC PROGRESSION

Hello MyRankers, Here is the explanation of Geometric Progression......

• A sequence of non-zero numbers is called a geometric progression (abbreviated as G.P.). If the ratio of a term and the term preceding  to it is always a constant quantity.
• The constant ratio is called the common ratio of the G.P.
• In other words, a sequence,  is called a geometric progression

                                                

GEOMETRIC SERIES:

If  a1,a2 ,a3,...an,... are in  G.P., then the expression a1+a2+a3+...an+...  is called a geometric series.

SELECTION OF TERMS IN G.P:

Sometimes it is required to select a finite number of terms in G.P. It is always convenient if we select the terms in the following manner: 

If the product of the numbers is not given, then the numbers are taken as 

PROPERTIES OF GEOMETRIC PROGRESSIONS:

PROPERTY I :

If all the terms of a G.P .are to be multiplied or divided by the same non-zero constant, then it remains a G.P. with the same common ratio.

PROPERTY II :

The reciprocals of the terms of a given G.P. form a G.P.

PROPERTY III :

If each term of  a G.P. is raised to the same power, the resulting sequence also forms a G.P.

PROPERTY IV: 

In a finite G.P. the product of the terms equidistant from the beginning and the end is always same and is equal to the product of the first and last term.

PROPERTY V :Three non-zero numbers a,b,c are in G.P. if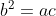    

PROPERTY VI :

If the terms of a given G.P. are chosen at regular intervals, then the new sequence so formed also forms a G.P.

PROPERTY VII :

If be a G.P of non-zero non-negative terms, then
     log a1, log a2,...logan,...is an A.P. and  viceversa.

SUM OF n TERMS OF A G.P:

The sum of n terms  of a G.P. with first term ‘a’ and  common ratio ‘r’ is given by 

If l is the last term of the G.P., then

** If n geometric means are inserted between two quantities, then the product of n geometric means is the nth power of the single geometric mean between the two quantities.

RELATION BETWEEN ARITHMETIC MEAN AND GEOMETRIC MEAN:

PROPERTY I:

If  A and G are respectively arithmetic and geometric means between two positive numbers a and b, then A > G.

PROPERTY II:

If A and G are respectively arithmetic and geometric means between two positive quantities a and b, then the quadratic equation having a,b as its roots is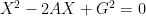  

PROPERTY III:

If A and G be the A.M and G.M. between two positive numbers, then the numbers are