Number of Atoms in a Unit Cell

No: of atoms per unit cell:

Position of Atoms in the Unit Cell	Contribution towards One Unit Cell
Corners	⅛
Edges	¼
Face centered	½
Body Centered	1

Primitive cell:

8 atoms at corners

So no. of atoms per cell = 8 x ⅛ = 1

Body centered:

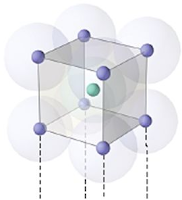
Total atoms at corners = 8

1 atom at centre

So total no: of atoms per unit cell = (8 x ⅛) + 1 = 2

Face centered unit cell:

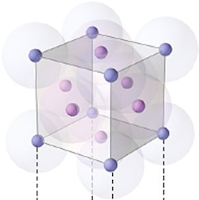
No: of atoms at corner = 8

No: of atoms at face = 6

So total no: of atoms per unit cell = (8 x ⅛) + (6 x ½) = 4

Crystal Radius:

Simple Cube:

a = 2r

r = a/2

Face Centered:

b = 4r

b² = a² + a²

16r² = 2a²

a = √8 r

a = 2√2 r

r = a/2√2

Body Centered:

b² = a² + a²

c² = a² + b²

c² = 3a²

c = √3 a

a = 4r/√3

r = √3a/4

Coordination number of unit cell: The number of nearest neighbors that a particle has a crystal lattice is called Coordination number:

1) For simple coordination number = 6

2) For Face centered cubic lattice = 12

3) For Body centered cubic lattice = 8