This is row-by-column multiplication
value for finding the product of two determinants and it is same as the rule of
multiplication of two matrices. Since the value of a determinant does not alter
by interchanging the rows and columns. So, we can also follow the row-by-row or
the column –by-row or column-by-column multiplication rule.
We have,









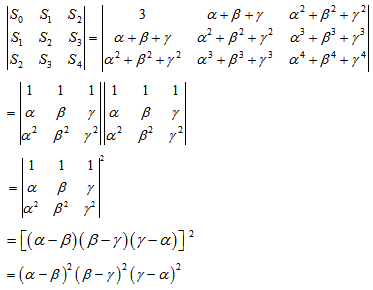
No comments:
Post a Comment