Common Tangents

Now we discuss the number of common tangents that exist for the cases specified in the section.

Case (i): Each of the given pair of circles lies in the exterior of the other i.e. C₁C₂ > r₁ + r₂.

Sub case (i): r₁ ≠ r₂ (r₁, r₂ are radii of the circles)

In this case, there is a possibility of having two pairs of common tangents. The pair of common tangents intersecting at a point on the line segment  is called transverse pair of common tangents and the pair of common tangents intersecting at a point not in  is called as direct pair of common tangents. The points P, Q are collinear with the centres C₁ and C₂ of given circles. The point of intersection of transverse pair of common tangents P is called the internal centre of similitude and the point of intersection of direct pair of common tangents Q is called external centre of similitude. Note that P divides C₁C₂ in the ratio r₁ : r₂ internally and Q divides  in the same ratio externally. Also note that C₁C₂ > r₁ + r₂. In this case the number of distinct common tangents is 4.

Sub case (ii):  > r₁ + r₂ and r₁ = r₂. In this case the direct common tangents are parallel.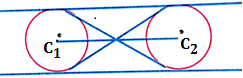

To find the equations of parallel common tangents, suppose the tangents equation as y = mx + c. The slope m = slope of C₁C₂ from this fact the value of m is known  (Radius is equal to perpendicular distance)

Using the above equation we can find C. In this case the number of common tangents is 4.

Case (ii):  = r₁ + r₂

Given circles touch each other externally. 

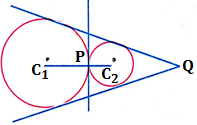
In this case the internal centre of similitude P is the point of contact of two given circles. At P there is only one common tangent. Through Q, there will be two common tangents. In this case the number of common tangents is 3.

Case (iii): |r₁ - r₂| <  < r₁ + r₂

(i.e., given circles intersecting each other)

In this case the internal centre of similitude does not exist. Only two common tangents through Q can be drawn.

Case (iv): C₁C₂ = |r₁ - r₂|

(i.e., given circles touch each other internally)

In this case internal centre of similitude does not exist. Only one common tangent exists at Q. Thus the number of common tangents in the present case is one.

Case (v):  < |r₁ - r₂|

(i.e., one circle lies entirely in the interior of the other circle)

In this case the number of common tangents is zero.