Property
1:
Let A = [aij] be a square matrix of order
then the sum of the
product of elements of any row (columns) with their cofactors is always equal
to |A| or det (A) i.e,
Property
2:
Let A = [aij] be a square matrix of order
n, then the sum of the product of elements of any row (column) with the
cofactors of the corresponding elements of some other row (column) is zero.
Property
3:
Let A = [aij] be a square matrix of order
n then |A|=|AT|.
Ex:
The value of a determinant remains unchanged if its
rows and columns are interchanged.
Property
4:
Let A = [aij] be a square matrix of order
n (≥ 2) and let B be a matrix obtained from A by interchanging any two rows
(columns) of A then |B|= -|A|.
Ex:
Property
5:
If any two rows (columns) of a square matrix A = [aij]
of order n (≥ 2) are identical. Then its determinant is zero i.e., |A|= 0.
Ex:
Property
6:
Let A = [aij] be a square matrix of order
n, and let B be the matrix obtained from A by multiplying each element of a row
(column) of A by scalar K then |B|= K|A|.
Ex:
Let A = [aij] be a square matrix of order
n, then |KA|= Kn|A|.
Property
7:
If each element of a row (column) of a determinant
is a sum of two terms, then determinant can be written as sum of two determinants.
Ex:
Property
8:
If each element of a row (column) of a determinant
is multiplied by the same constant and then added to the corresponding elements
of some other row (column), then the value of the determinant remains same.
Ex:
Obtained after C2 → C2 + 2C1
+3C3
Property
9:
If each element of a row (column) of a determinant
zero, then its value is zero.
Ex:
Property
10:
If A = [aij] is a diagonal matrix of
order n (≥ 2), then |A|= a11, a22, a33 … anm.
Property
11:
If A and B are square matrices of the same order,
then |AB|=|A||B|.
Property
12:
If A = [aij] is triangular matrix of
order n, then |A|= a11, a22, a33 … anm.
Ex:
Property
13:
If A is a non-singular square matrix of order n,
then |adj A| = |A|n-1.
Property
14:
If A is a skew-symmetric matrix of odd order, then
|A| = 0.
Property
15:
If A is a skew-symmetric matrix of even order, then
|A| is a perfect square.


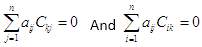









No comments:
Post a Comment